How To Understand How Neural Networks Work

Delving into the fascinating world of artificial neural networks, this guide provides a comprehensive overview of their structure, function, and practical applications. From the fundamental concepts of neurons and layers to the intricate mathematical operations driving their learning process, we’ll explore the key components and mechanisms behind these powerful computational models. This journey will illuminate how neural networks learn from data, adapt to new information, and achieve remarkable performance in diverse fields.

This guide will equip you with a solid understanding of neural networks, enabling you to appreciate their versatility and potential in various applications. We will cover the essentials, from the basics of network architectures to troubleshooting and visualization techniques. This exploration aims to empower readers to approach neural networks with confidence and a deeper understanding.

Introduction to Neural Networks

Artificial neural networks (ANNs) are computational models inspired by the structure and function of the human brain. They consist of interconnected nodes, or “neurons,” organized in layers, enabling them to learn complex patterns and relationships from data. This learning process allows ANNs to make predictions or classifications on new, unseen data. ANNs have found widespread applications in various fields, including image recognition, natural language processing, and financial modeling.Neural networks excel at identifying intricate relationships within data that traditional methods might miss.

This ability stems from their iterative learning process, adjusting internal parameters to optimize their performance. Their capacity to generalize from training data to novel situations distinguishes them from other approaches.

Fundamental Concepts

Neural networks operate on the principle of weighted connections between neurons. Each connection carries a weight that modifies the strength of the signal passing through it. The neurons process this input, combining it with their internal state, and produce an output. This process is repeated across multiple layers, allowing the network to progressively extract higher-level features from the input data.

Types of Neural Networks

Different types of neural networks are designed for various tasks. Feedforward networks, for example, process data in a single direction, from input to output, without feedback loops. Recurrent neural networks (RNNs), on the other hand, have loops within their structure, enabling them to process sequential data, such as text or time series.

Network Structure and Components

A neural network typically consists of interconnected layers of neurons. The input layer receives the initial data, hidden layers perform intermediate computations, and the output layer produces the final result. Connections between neurons are weighted, and these weights are adjusted during the learning process. Each neuron sums the weighted inputs, applies an activation function, and then transmits the output to the next layer.

Analogy

Imagine a team of experts trying to identify a specific type of fruit from its description. Each expert (neuron) has a particular area of expertise (e.g., shape, color, texture). They each evaluate the description (input data) and contribute their assessment (output) to the final decision (output layer). The team’s expertise is adjusted (weights) over time as they analyze more examples, improving their accuracy in recognizing the fruit.

This adjustment in expertise (weight updates) mirrors the learning process in neural networks.

Understanding the Learning Process

Neural networks, unlike traditional algorithms, learn from data rather than being explicitly programmed. This learning process involves adjusting the network’s internal parameters, known as weights, to optimize its performance on a given task. This iterative adjustment, driven by algorithms, is crucial for the network to generalize from the training data and perform well on unseen data.The core of this learning process lies in the network’s ability to identify patterns and relationships within the data.

By adjusting the connections between neurons, the network progressively refines its understanding of these patterns, leading to improved accuracy and predictive capabilities. This iterative process is essential for the network to develop an internal representation of the input data, allowing it to make informed decisions on new, unseen data.

Training Data and its Role

The training data serves as the foundation for the learning process. It comprises a set of input-output pairs that represent the desired behavior of the network. Each input corresponds to a specific output, and the network’s goal is to learn the mapping between them. A well-chosen and representative training dataset is essential for the network to generalize effectively and avoid overfitting.

Overfitting occurs when the network memorizes the training data rather than learning the underlying patterns, leading to poor performance on unseen data.

Learning Algorithms

Different learning algorithms employ various strategies to adjust the network’s weights. A crucial algorithm is backpropagation, a method for calculating the gradient of the error function with respect to the network’s weights. This gradient provides the direction and magnitude of the adjustments needed to minimize the error.

Backpropagation

Backpropagation, a cornerstone of neural network training, involves calculating the error at the output layer and propagating it backward through the network to adjust the weights. The algorithm calculates the difference between the predicted output and the actual output for each training example. This error signal is then used to update the weights in a way that reduces the error for future inputs.

This process is repeated iteratively until the network achieves acceptable accuracy on the training data.

The essence of backpropagation lies in its gradient descent approach. It systematically adjusts the weights in the direction that minimizes the error, effectively searching for the optimal configuration. The algorithm is crucial for training complex neural networks with many layers and connections.

Weight Adjustment

The core of the learning process is the adjustment of the weights. By systematically updating these weights, the network refines its ability to map inputs to outputs. The magnitude and direction of the weight adjustment are determined by the gradient calculated during backpropagation. This iterative process continues until the network’s output consistently aligns with the desired output for the training data.

Different Learning Strategies

Various learning strategies exist, each with its own strengths and weaknesses. Stochastic gradient descent (SGD) updates weights after each training example, which can be faster but less stable. Batch gradient descent updates weights after processing a batch of examples, leading to a more stable but slower learning process. Mini-batch gradient descent combines the advantages of both, updating weights after processing a mini-batch of examples.

Choosing the appropriate strategy depends on the specific characteristics of the dataset and the computational resources available.

Challenges and Limitations

Training neural networks can present challenges. Finding the optimal balance between model complexity and the size of the training data is crucial. Overfitting, as mentioned earlier, is a significant concern, where the model learns the training data too well, failing to generalize to new data. Another challenge is the computational cost, particularly for large networks and datasets.

Gradient vanishing and exploding are additional issues that can hinder training effectiveness.

Key Components of a Neural Network

Neural networks, inspired by the human brain, are complex systems capable of learning from data. Understanding their fundamental components is crucial to grasping their functionality. These components, working in concert, allow the network to identify patterns, make predictions, and solve complex problems.The core building blocks of a neural network are interconnected nodes, or neurons, organized in layers. Activation functions introduce non-linearity, enabling the network to learn complex relationships.

Weights and biases adjust the strength of connections between neurons, refining the network’s understanding of the data. These elements interact to produce a final output, representing the network’s learned understanding.

Neurons: The Basic Processing Units

Neurons are the fundamental processing units within a neural network. Each neuron receives input from other neurons, processes it, and then transmits the output to other neurons in the subsequent layer. This process is repeated across layers, culminating in the network’s final output.

Activation Functions: Introducing Non-linearity

Activation functions introduce non-linearity into the network’s operation. Without them, the network would essentially be a linear transformation, limiting its ability to learn complex patterns. These functions map the weighted sum of inputs to an output, determining whether a neuron should be activated or not. Common activation functions include sigmoid, ReLU (Rectified Linear Unit), and tanh. These functions introduce non-linearity and enable the network to learn more complex relationships in the data.

Weights and Biases: Controlling the Strength of Connections

Weights and biases are crucial parameters that control the strength and direction of connections between neurons. Weights represent the strength of the connection between two neurons, determining how much influence one neuron has on another. Biases, on the other hand, act as a threshold for the neuron’s activation. They determine the minimum input required for the neuron to activate.

By adjusting these weights and biases, the network learns to recognize patterns and make accurate predictions. This adjustment is a key aspect of the learning process.

Interaction of Components: Producing an Output

The interaction between neurons, activation functions, weights, and biases is the essence of a neural network’s operation. A neuron receives input signals from other neurons, weighted according to the strength of the connections. These weighted signals are summed, along with a bias term. The activation function then transforms this sum into an output signal, which is then passed on to the next layer.

This process repeats across multiple layers, ultimately producing the network’s final output.

Visual Representation of a Neuron

Imagine a neuron as a small circle. Numerous input connections, represented by lines, lead to this circle. Each line corresponds to a specific weight. The weights are represented by values associated with each line. These weights multiply the incoming signal from other neurons.

The sum of all weighted inputs, plus a bias, is then passed through an activation function (often shown as a separate block or function applied to the sum). The resulting output from the activation function is then transmitted to other neurons in the subsequent layer. This interconnected web of neurons and connections forms the neural network.

Mathematical Basis

Neural networks rely heavily on mathematical operations to process information and learn from data. These operations form the core of how these networks function, enabling them to identify patterns and make predictions. Understanding the mathematical underpinnings provides a deeper insight into the inner workings of neural networks.The fundamental mathematical operations, such as matrix multiplication and linear algebra, are crucial in calculating outputs and updating network parameters.

These calculations are repeated during the learning process, adjusting the network’s structure to optimize its performance on the given task.

Matrix Multiplication

Matrix multiplication is a cornerstone of neural network computations. It allows for efficient handling of multiple inputs and weights simultaneously. Consider a layer of neurons receiving multiple input values. Each neuron’s output is a weighted sum of these inputs. Matrix multiplication effectively performs these calculations for all neurons in the layer in a concise manner.

This operation takes the input vector and the weight matrix as input, resulting in an output vector representing the weighted sum for each neuron.

Linear Algebra

Linear algebra is fundamental to understanding the structure and operations within neural networks. Concepts like vectors, matrices, and tensors are essential for representing data, weights, and activations. Vectors represent input data, matrices store weights between layers, and tensors encapsulate multi-dimensional data. Linear algebra operations enable calculations like matrix multiplications, which are critical for propagating input through the network.

Key Equations and Formulas

Neural networks utilize several key equations and formulas to perform calculations. The weighted sum of inputs, commonly represented as z, is a crucial step. This sum is then passed through an activation function (e.g., sigmoid, ReLU). This transformation, often denoted as a(z), determines the output of the neuron. The key formula is:

a = activation_function(z)

where z = Σ (weight _i – input _i)The backpropagation algorithm, used for updating network weights, relies on gradient calculations. Gradients measure the rate of change of the cost function with respect to the network’s weights. These gradients are calculated using techniques like the chain rule, a fundamental concept in calculus. This calculation is essential for adjusting weights to reduce the error between predicted and actual outputs.

Gradients and Training

Gradients play a vital role in training neural networks. They provide the direction and magnitude of adjustments needed to optimize the network’s performance. Calculating gradients, often using backpropagation, allows the network to iteratively adjust its weights, leading to better predictions. The magnitude of the gradient indicates the steepness of the cost function at a particular point, influencing the size of the weight update.

The direction of the gradient points toward the region of the cost function with lower values, guiding the optimization process.

Mathematical Operations and Learning

The mathematical operations used in neural networks directly contribute to the learning process. Matrix multiplication efficiently calculates outputs for multiple neurons simultaneously. Linear algebra operations allow for the effective representation and manipulation of data within the network. Gradients, calculated through backpropagation, provide the direction for adjusting weights to reduce errors. These iterative updates, guided by gradients, enable the network to progressively learn patterns from the data, leading to improved predictions and performance.

Practical Applications

Neural networks are transforming numerous industries by automating complex tasks and enabling sophisticated decision-making. Their ability to learn from data and identify patterns makes them invaluable tools for a wide range of applications, from image recognition to natural language processing. This section will delve into the diverse applications of neural networks and illustrate their impact on various fields.

Real-World Applications

Neural networks are proving remarkably effective in numerous real-world applications. From diagnosing medical conditions to predicting market trends, these systems demonstrate adaptability and accuracy. Their versatility stems from the ability to adjust their internal parameters to fit specific tasks.

Image Recognition

Image recognition is a prime example of neural networks’ power. These networks can be trained to identify objects, faces, or even emotions within images. Convolutional neural networks (CNNs) are particularly well-suited for image-related tasks due to their hierarchical structure that effectively captures intricate patterns within visual data. CNNs excel at identifying subtle features within images, enabling accurate classification and detection.

For instance, a CNN can be trained to identify cancerous cells in medical images with a high degree of accuracy, significantly aiding in early diagnosis.

Natural Language Processing

Neural networks are revolutionizing natural language processing (NLP). They excel at tasks like machine translation, sentiment analysis, and text summarization. Recurrent neural networks (RNNs) and transformers are prominent in NLP applications, effectively handling sequential data like text. RNNs process text sequentially, while transformers analyze the entire text simultaneously, allowing for more nuanced understanding and context. These advancements allow for more human-like communication with machines.

Applications in Other Domains

Beyond image recognition and NLP, neural networks are finding applications in various other fields. In finance, they can predict market trends and identify fraudulent activities. In healthcare, they can assist in diagnosis, drug discovery, and personalized treatment plans. These systems leverage vast datasets to identify patterns and insights that humans might miss. For instance, neural networks can analyze patient records to predict the likelihood of certain diseases, allowing for proactive interventions.

Summary Table of Applications

Application	Description	Benefits
Image Recognition	Identifying objects, faces, and other features in images.	Improved accuracy in medical diagnosis, enhanced security systems, and improved quality control in manufacturing.
Natural Language Processing	Understanding and generating human language.	Enabling more natural and efficient communication between humans and machines, assisting in language translation, and automating customer service tasks.
Finance	Predicting market trends, identifying fraudulent activities, and assessing credit risk.	Improved risk management, more accurate investment strategies, and reduced fraud losses.
Healthcare	Assisting in diagnosis, drug discovery, and personalized treatment plans.	Early disease detection, improved treatment outcomes, and personalized medicine.

Common Architectures

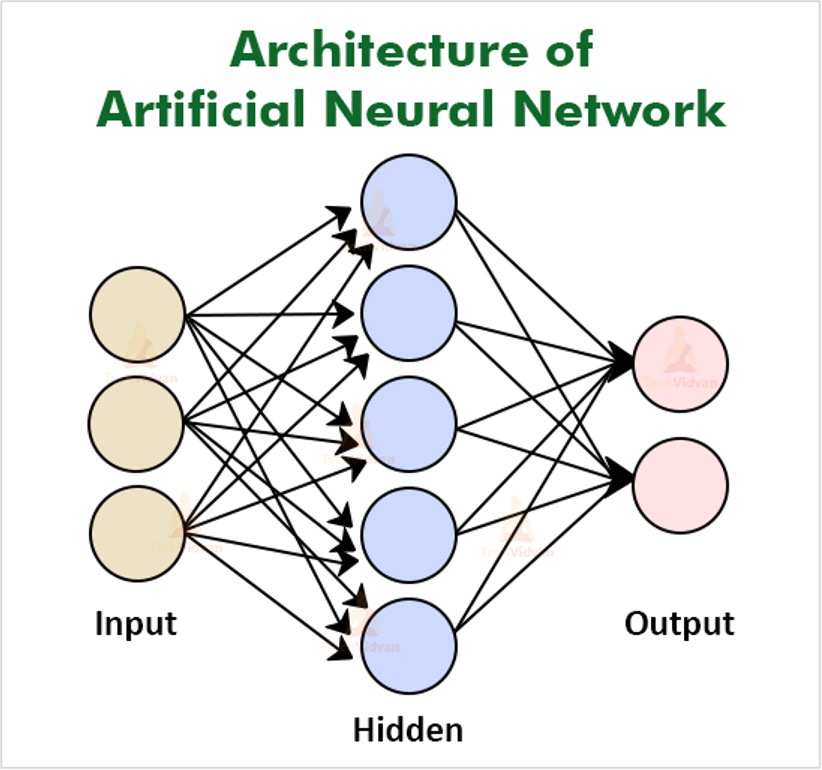
Neural networks come in diverse architectures, each tailored for specific tasks. Understanding these architectures is crucial for selecting the right network for a given problem. Different architectures excel at different types of data and exhibit varying computational complexities. This section explores prevalent architectures like Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), highlighting their strengths, weaknesses, and suitable applications.

Convolutional Neural Networks (CNNs)

CNNs are particularly well-suited for processing grid-like data, such as images and videos. Their unique structure leverages local connections and shared weights to extract hierarchical features from the input data. This approach significantly reduces the number of parameters compared to fully connected networks, making CNNs computationally efficient for large datasets.

• Strengths: CNNs excel at tasks requiring spatial reasoning, like image classification, object detection, and image segmentation. Their ability to extract hierarchical features allows them to identify complex patterns in images.
• Weaknesses: CNNs struggle with sequential data, making them unsuitable for tasks like natural language processing or time series analysis. They can also be computationally expensive for extremely large images or videos.
• Use Cases: Image recognition, object detection, image segmentation, medical image analysis, and facial recognition.

Recurrent Neural Networks (RNNs)

RNNs are designed to handle sequential data, such as text, speech, and time series. Their unique structure allows them to maintain a “memory” of previous inputs, enabling them to process data with dependencies across time steps.

• Strengths: RNNs excel at tasks requiring understanding of context and sequence, such as machine translation, text generation, speech recognition, and natural language understanding. Their ability to capture temporal dependencies makes them ideal for these applications.
• Weaknesses: RNNs can suffer from the vanishing gradient problem, which limits their ability to learn long-range dependencies. Training RNNs can also be computationally intensive for lengthy sequences.
• Use Cases: Natural language processing (NLP), machine translation, speech recognition, time series forecasting, and handwriting recognition.

Comparison of Architectures

Architecture Type	Strengths	Weaknesses	Use Cases
Convolutional Neural Networks (CNNs)	Excellent at extracting hierarchical features from grid-like data; computationally efficient for large datasets; excels at spatial reasoning.	Struggles with sequential data; computationally expensive for extremely large inputs.	Image recognition, object detection, image segmentation, medical image analysis.
Recurrent Neural Networks (RNNs)	Capable of handling sequential data; can capture temporal dependencies; suitable for tasks requiring context understanding.	Can suffer from vanishing gradient problem; computationally intensive for long sequences; can be challenging to train.	Natural language processing, machine translation, speech recognition, time series forecasting.

Troubleshooting and Debugging

Troubleshooting neural networks involves identifying and resolving issues during the training and deployment phases. Effective debugging is crucial for ensuring optimal model performance and preventing costly errors. This process often requires a systematic approach, combining theoretical understanding with practical techniques.Understanding the source of errors is paramount in achieving successful model development. Careful analysis of model behavior and performance metrics is vital for identifying problems.

Techniques for evaluating model performance and diagnosing problems form the cornerstone of efficient debugging.

Common Pitfalls in Training

Incorrect hyperparameter settings, insufficient data, and inappropriate network architecture can hinder training progress. These issues are often the source of slow convergence, poor generalization, or overfitting.

• Overfitting occurs when a model learns the training data too well, capturing noise and irrelevant details. This results in high accuracy on the training set but poor performance on unseen data. Regularization techniques, like dropout and L1/L2 penalties, can mitigate this issue.
• Underfitting happens when the model is too simple to capture the underlying patterns in the data. This leads to poor performance on both training and testing sets. Increasing the complexity of the network architecture or adding more training data can address this problem.
• Vanishing/Exploding Gradients These issues arise during backpropagation. Vanishing gradients occur when gradients become extremely small, hindering the learning process. Exploding gradients happen when gradients become extremely large, making the learning process unstable. Techniques like gradient clipping and different activation functions can help mitigate these challenges.

Evaluating Model Performance

Quantitative assessment of model performance is essential for identifying potential issues. Various metrics provide insights into the model’s accuracy, precision, recall, and other relevant measures.

• Accuracy measures the percentage of correctly classified instances. High accuracy does not guarantee a robust model. Consider other metrics like precision and recall.
• Precision measures the proportion of correctly identified positive instances out of all predicted positive instances. A high precision indicates that the model is less likely to misclassify negative instances as positive.
• Recall measures the proportion of correctly identified positive instances out of all actual positive instances. High recall ensures that the model does not miss many positive cases.
• F1-score is the harmonic mean of precision and recall, providing a balanced measure of performance.

Diagnosing and Fixing Model Problems

Debugging strategies involve analyzing training logs, visualizing model outputs, and comparing predicted values with actual values.

• Analyzing Training Logs: Examining training loss and accuracy curves reveals trends in the learning process. Sudden changes or plateaus in these curves can indicate problems like vanishing gradients, overfitting, or insufficient training data.
• Visualizing Model Outputs: Visualizing predictions against ground truth values provides insights into the model’s decision-making process. Inconsistencies or patterns in errors can help pinpoint the source of the problem.
• Comparing Predictions with Actual Values: Detailed analysis of misclassified instances highlights areas where the model struggles. Identifying patterns in these misclassifications provides valuable clues for improvement.

Debugging Flowchart

The following flowchart illustrates a systematic approach to debugging neural network models.

[A flowchart illustrating the debugging process would be included here. It would start with identifying a problem, proceed to analyzing training logs, model outputs, comparing predictions, and then suggest corrective actions based on the analysis. It would show branching paths for different types of problems, such as overfitting, underfitting, vanishing gradients, etc.]

Visualization and Interpretation

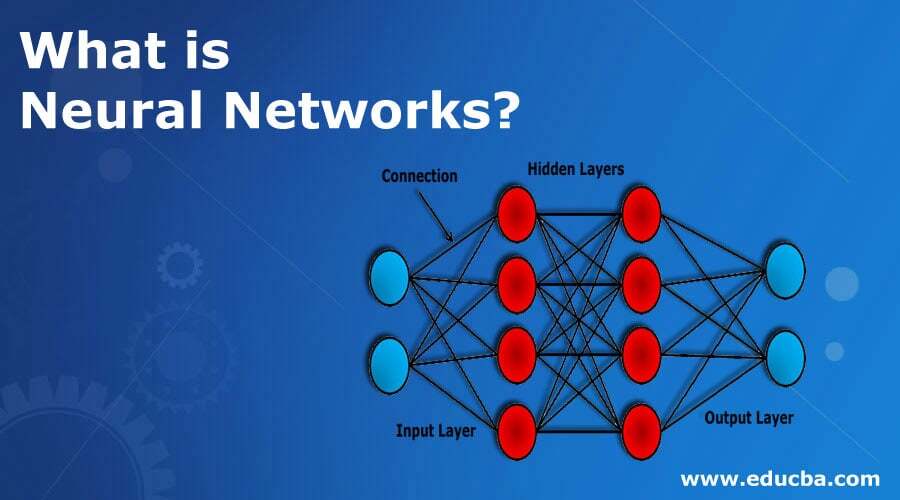
Understanding the internal workings of a neural network and interpreting its results are crucial for validating its performance and gaining insights into its decision-making process. Visualizations help in identifying potential issues, understanding data flow, and assessing the network’s structure and behavior. This section details methods for achieving these goals.

Methods for Visualizing Internal Workings

Visualization techniques offer a powerful means of comprehending neural network behavior. They allow for a clear representation of the network’s structure, data flow, and internal computations.

• Network Architecture Visualization: Representing the network’s structure, including the number of layers, neurons per layer, and connections between them. This visual representation helps in identifying potential bottlenecks or inefficiencies. A diagram of a multi-layer perceptron (MLP) clearly shows the input layer, hidden layers, and output layer, with connections between neurons. This helps in understanding the complexity and depth of the network.

• Activation Visualization: Displaying the activation values of neurons at different layers during the forward pass. These values indicate how each neuron responds to the input data. This allows for the analysis of how information is processed through the network. For example, if an image is classified, visualization of activation values in the convolutional layers can highlight which parts of the image the network focuses on.

• Weight Visualization: Representing the weights of the connections between neurons. This visualization can reveal patterns in the learned relationships between inputs and outputs. For instance, in image recognition, visualizing weights in the convolutional layers might show features like edges, corners, or textures being learned by the network. Color-coding can highlight the importance of different weights.

Interpreting Neural Network Results

Understanding the reasoning behind a neural network’s predictions is essential for trust and deployment.

• Feature Importance Analysis: Identifying the input features that significantly contribute to the network’s output. This can be achieved through techniques like gradient-based methods, which highlight the importance of different input features in determining the network’s output. For example, in a loan application, understanding which features (credit score, income, etc.) are most important for approval can provide insights and transparency.
• Prediction Explanation: Providing a clear and concise explanation for a specific prediction. Techniques like saliency maps can visualize which parts of the input data are most influential in generating a particular prediction. This helps in understanding the network’s decision-making process. For example, in a medical diagnosis, understanding the reasons for a disease prediction can be crucial for patient care.

• Error Analysis: Examining the errors made by the network to identify areas for improvement. Visualizing misclassified examples and comparing them to correctly classified examples can highlight patterns in the errors and guide adjustments to the network. This approach helps to fine-tune the model and enhance its accuracy.

Visualizing Data Flow Through the Network

Visualizing the flow of data through a neural network helps understand how the network processes information.

• Activation Flow Diagrams: Visualizing the progression of activations from the input layer through hidden layers to the output layer. These diagrams demonstrate how the network transforms the input data at each layer. For instance, in a natural language processing task, visualizing the activation flow can highlight how different words or phrases influence the network’s output.

Understanding the Decision-Making Process

The interpretation of a neural network’s decision-making process can be challenging.

• Activation Path Visualization: Visualizing the path taken by the activations through the network for a specific input. Highlighting the neurons that contributed significantly to the output can provide insights into the network’s reasoning process. For example, in image classification, visualizing the activation paths for different classes can highlight which features are used to distinguish those classes.

Examples

• Image Recognition: Visualizing the activations in a convolutional neural network (CNN) processing an image can highlight the areas of the image that the network focuses on during classification. For example, in identifying cats in images, the network might highlight the cat’s fur patterns or eyes as crucial features.
• Natural Language Processing (NLP): In a sentiment analysis task, visualizing the activations of a recurrent neural network (RNN) processing a sentence can reveal which words or phrases contribute most to the overall sentiment. For example, if the network determines that a sentence expresses positive sentiment, visualizing activations for words like “excellent” or “wonderful” can help clarify the network’s decision.

Resources and Further Learning

Expanding your knowledge of neural networks requires access to diverse resources. This section provides a selection of research papers, online courses, libraries, and frameworks to facilitate deeper learning and practical implementation. These resources will enable you to explore the theoretical underpinnings and practical applications of neural networks more thoroughly.

Research Papers and Articles

A wealth of valuable information exists in academic research papers. These papers often delve into the theoretical foundations and advancements of neural networks. Staying updated with the latest research is essential for understanding the evolving landscape of this field.

• Many influential papers on neural networks are available through reputable academic databases like arXiv and JSTOR. Searching for s like “deep learning,” “convolutional neural networks,” or “recurrent neural networks” can yield relevant results.
• Specialized journals such as “IEEE Transactions on Neural Networks and Learning Systems” and “Nature Machine Intelligence” frequently publish cutting-edge research papers.

Online Courses and Tutorials

Numerous online platforms offer comprehensive courses and tutorials on neural networks. These resources often combine theoretical explanations with practical exercises and hands-on projects.

• Coursera and edX provide courses on deep learning and neural networks from leading universities and institutions, offering structured learning paths and certificates.
• Udacity and fast.ai provide focused tutorials and specialization tracks, often with a practical emphasis on implementing neural networks in various domains.
• YouTube channels like 3Blue1Brown offer engaging visual explanations of neural network concepts, making complex topics more accessible.

Libraries and Frameworks

Specialized libraries and frameworks significantly streamline the implementation of neural networks. These tools provide pre-built functionalities for constructing, training, and evaluating models.

• TensorFlow and PyTorch are two prominent Python libraries for building and training neural networks. They offer extensive functionalities for defining complex architectures, optimizing models, and managing computational resources efficiently.
• Keras is a high-level API that simplifies the development process by abstracting away many implementation details. It can be used with TensorFlow or Theano as backend, offering flexibility and ease of use.

Key Resources

This compilation Artikels key resources for individuals seeking a deeper understanding of neural networks.

Category	Resource	Description
Online Courses	Coursera, edX	Structured learning paths, often with certificates.
Libraries/Frameworks	TensorFlow, PyTorch, Keras	Streamline neural network implementation.
Research Papers	arXiv, JSTOR, IEEE Transactions on Neural Networks and Learning Systems	Access to cutting-edge research in the field.

Ultimate Conclusion

In conclusion, this comprehensive guide has explored the multifaceted world of neural networks. We’ve examined their inner workings, from the fundamental principles of learning and architecture to real-world applications and troubleshooting strategies. By understanding the key components, mathematical basis, and practical implementations, you are now equipped to engage with neural networks with greater confidence and insight. This journey through the world of neural networks should provide a strong foundation for further exploration and application.